Konsument, mając dochód, chce go wydać i oczywiście z maksymalną korzyścią. Korzyść rozumiana jest w sensie systemu preferencji lub funkcji użyteczności. W naszej pracy przyjrzeliśmy się, jak zoptymalizować wybór konsumenta.
Zadanie optymalizacji wyboru konsumenta
Istota optymalizacji wyboru konsumenta.
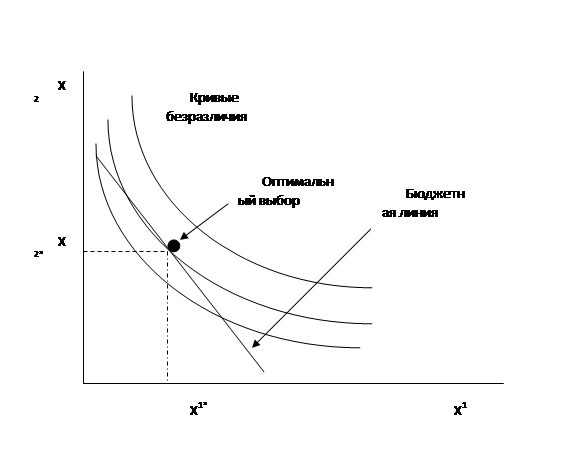
Wybór (X1 *, X2 *) jest optymalnym wyborem dla konsumenta. Wiele zestawów, które preferuje (X1 *, X2 *), a mianowicie zbiór, który znajduje się powyżej jego krzywej obojętności, nie przecina zbiorów, na które może sobie pozwolić, a mianowicie zbiorów w linii budżetowej. Tak więc zestaw (X1 *, X2 *) jest najlepszym zestawem, na który konsument może sobie pozwolić.
Aby rozważyć ten problem, należy użyć jako aplikacji ustalenia warunkowego ekstremum za pomocą mnożników Lagrange'a.
Jak wybierają indywidualni konsumenci, ile kupują każdego produktu, biorąc pod uwagę preferencje i ograniczenia budżetowe? Zakładamy, że konsumenci dokonują tego wyboru z racjonalnych powodów - wybierają produkty w taki sposób, aby zmaksymalizować satysfakcję, jaką otrzymują, biorąc pod uwagę ich ograniczony budżet.
Kwalifikujący się koszyk musi spełniać dwa warunki:
Powinien być w linii budżetowej. Dlaczego Należy pamiętać, że każdy koszyk na rynku po lewej stronie i poniżej linii budżetowej pozostawia pewną kwotę niewydanych dochodów, która, jeśli zostanie wydana, może zwiększyć zadowolenie klienta. Oczywiście konsumenci mogą - a czasami robią to - oszczędzać część swoich dochodów na przyszłą konsumpcję. Jednak na razie uprościmy sytuację, zakładając, że cały dochód zostanie wydany natychmiast. Należy również pamiętać, że żaden koszyk na rynku po prawej i powyżej linii budżetowej nie może zostać pozyskany przy istniejącym poziomie dochodów. Dlatego jedynym racjonalnym i wykonalnym wyborem jest koszyk w linii budżetowej.
Powinien on zapewnić konsumentowi najkorzystniejszą kombinację towarów i usług.
Te dwa warunki zmniejszają problem maksymalnego zadowolenia konsumenta z kwestii wyboru odpowiedniego punktu w linii budżetowej.
Jeśli przeanalizujemy graficznie problem wyboru konsumenta między jedzeniem a ubraniem, możemy stwierdzić, że kosz, który przynosi maksymalną satysfakcję, powinien leżeć na najwyższej krzywej obojętności odnoszącej się do linii budżetowej. W punkcie styczności linii budżetowej i krzywej obojętności nachylenie linii budżetowej jest dokładnie równe nachyleniu krzywej obojętności. Ponieważ krańcowa stopa substytucji (MRS) jest ujemna, odwrotność nachylenia krzywej obojętności, można powiedzieć, że zadowolenie osiąga maksimum (przy ograniczeniu budżetowym) w punkcie, w którym
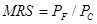
Zadanie optymalizacji wyboru konsumenta można uznać za zastosowanie metody znajdowania warunkowego ekstremum mnożników Lagrange'a.
Zakładamy, że każdy produkt ma cenę pi, a osoba ma dochód Q - pewną ilość pieniędzy, w ramach której działa, kupując zestaw towarów, których potrzebuje. Zakup zestawu towarów X = (xi, ..., xn) wymaga wydania pieniędzy w wysokości c (X) = pixi + ... + pnxn =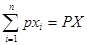 
Zatem jednostka może kupić tylko taki zestaw X, w którym PX≤Q. W konsekwencji zbiór zestawów dóbr dostępnych dla niego z przychodem Q. to B = B (P, Q) = {X; X≥0, PX≤Q}. Ten zestaw nazywa się zestawem budżetu. Zestaw budżetu jest ograniczony i zamknięty.
Dowód. Niech r = min pi, a następnie jak łatwo sprawdzić, czy X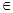 
B, następnie x≤Q / r dla i = 1, ..., n, tj. B jest ograniczone. Udowadniamy zamknięcie. Niech hk 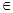B za każde k 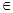N i Xk 
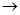Z. Następnie dzięki ciągłości funkcji liniowej
Pxk 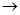PZ i, ponieważ PXk≤Q, następnie PZ≤Q. Dlatego Z 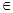B.
Przejdź do strony: 1 2
Jak wybierają indywidualni konsumenci, ile kupują każdego produktu, biorąc pod uwagę preferencje i ograniczenia budżetowe?
